力扣00064.最小路径和

发表于 分类于 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 9 分钟
最小路径和、数组、动态规划、矩阵、中等

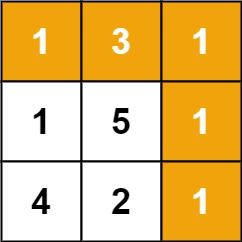
题目描述

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • 0 <= grid[i][j] <= 200

解决方法

C++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        dp[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
};

结果

执行用时 : 6 ms, 击败 75.52% 使用 C++ 的用户

内存消耗 : 12.29 MB, 击败 16.65% 使用 C++ 的用户

Java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
}

结果

执行用时 : 2 ms, 击败 94.43% 使用 Java 的用户

内存消耗 : 44.47 MB, 击败 22.64% 使用 Java 的用户

Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution(object):
    def minPathSum(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        m, n = len(grid), len(grid[0])
        dp = [[0] * n for _ in range(m)]
        dp[0][0] = grid[0][0]
        for i in range(1, m):
            dp[i][0] = dp[i-1][0] + grid[i][0]
        for j in range(1, n):
            dp[0][j] = dp[0][j-1] + grid[0][j]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
        return dp[m-1][n-1]

结果

执行用时 : 19 ms, 击败 94.35% 使用 Python 的用户

内存消耗 : 12.98 MB, 击败 82.03% 使用 Python 的用户

Python3

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dp = [[0] * n for _ in range(m)]
        dp[0][0] = grid[0][0]
        for i in range(1, m):
            dp[i][0] = dp[i-1][0] + grid[i][0]
        for j in range(1, n):
            dp[0][j] = dp[0][j-1] + grid[0][j]
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
        return dp[m-1][n-1]

结果

执行用时 : 46 ms, 击败 70.68% 使用 Python3 的用户

内存消耗 : 18.70 MB, 击败 40.45% 使用 Python3 的用户

C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int min(int a, int b) {
    return a < b ? a : b;
}
int minPathSum(int** grid, int gridSize, int* gridColSize) {
    int m = gridSize;
    int n = *gridColSize;
    int** dp = (int**)malloc(m * sizeof(int*));
    for (int i = 0; i < m; ++i) {
        dp[i] = (int*)malloc(n * sizeof(int));
    }
    dp[0][0] = grid[0][0];
    for (int i = 1; i < m; ++i) {
        dp[i][0] = dp[i-1][0] + grid[i][0];
    }
    for (int j = 1; j < n; ++j) {
        dp[0][j] = dp[0][j-1] + grid[0][j];
    }
    for (int i = 1; i < m; ++i) {
        for (int j = 1; j < n; ++j) {
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
        }
    }
    int result = dp[m-1][n-1];
    for (int i = 0; i < m; ++i) {
        free(dp[i]);
    }
    free(dp);
    return result;
}

结果

执行用时 : 9 ms, 击败 39.13% 使用 C 的用户

内存消耗 : 7.18 MB, 击败 65.60% 使用 C 的用户

C#

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
    public int MinPathSum(int[][] grid) {
        int m = grid.Length;
        int n = grid[0].Length;
        int[][] dp = new int[m][];
        for (int i = 0; i < m; ++i) {
            dp[i] = new int[n];
        }
        dp[0][0] = grid[0][0];
        for (int i = 1; i < m; ++i) {
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for (int j = 1; j < n; ++j) {
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }
        for (int i = 1; i < m; ++i) {
            for (int j = 1; j < n; ++j) {
                dp[i][j] = Math.Min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
            }
        }
        return dp[m-1][n-1];
    }
}

结果

执行用时 : 76 ms, 击败 65.48% 使用 C# 的用户

内存消耗 : 43.01 MB, 击败 20.84% 使用 C# 的用户

JavaScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function(grid) {
    const m = grid.length;
    const n = grid[0].length;
    const dp = new Array(m);
    for (let i = 0; i < m; ++i) {
        dp[i] = new Array(n);
    }
    dp[0][0] = grid[0][0];
    for (let i = 1; i < m; ++i) {
        dp[i][0] = dp[i-1][0] + grid[i][0];
    }
    for (let j = 1; j < n; ++j) {
        dp[0][j] = dp[0][j-1] + grid[0][j];
    }
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
        }
    }
    return dp[m-1][n-1];
};

结果

执行用时 : 54 ms, 击败 95.33% 使用 JavaScript 的用户

内存消耗 : 51.90 MB, 击败 18.70% 使用 JavaScript 的用户

TypeScript

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function minPathSum(grid: number[][]): number {
    const m = grid.length;
    const n = grid[0].length;
    const dp: number[][] = new Array(m);
    for (let i = 0; i < m; ++i) {
        dp[i] = new Array(n);
    }
    dp[0][0] = grid[0][0];
    for (let i = 1; i < m; ++i) {
        dp[i][0] = dp[i-1][0] + grid[i][0];
    }
    for (let j = 1; j < n; ++j) {
        dp[0][j] = dp[0][j-1] + grid[0][j];
    }
    for (let i = 1; i < m; ++i) {
        for (let j = 1; j < n; ++j) {
            dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
        }
    }
    return dp[m-1][n-1];
}

结果

执行用时 : 52 ms, 击败 99.50% 使用 TypeScript 的用户

内存消耗 : 52.69 MB, 击败 16.42% 使用 TypeScript 的用户

PHP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {

    /**
     * @param Integer[][] $grid
     * @return Integer
     */
    function minPathSum($grid) {
        $m = count($grid);
        $n = count($grid[0]);
        $dp = array();
        for ($i = 0; $i < $m; ++$i) {
            $dp[$i] = array();
        }
        $dp[0][0] = $grid[0][0];
        for ($i = 1; $i < $m; ++$i) {
            $dp[$i][0] = $dp[$i-1][0] + $grid[$i][0];
        }
        for ($j = 1; $j < $n; ++$j) {
            $dp[0][$j] = $dp[0][$j-1] + $grid[0][$j];
        }
        for ($i = 1; $i < $m; ++$i) {
            for ($j = 1; $j < $n; ++$j) {
                $dp[$i][$j] = min($dp[$i-1][$j], $dp[$i][$j-1]) + $grid[$i][$j];
            }
        }
        return $dp[$m-1][$n-1];
    }
}

结果

执行用时 : 19 ms, 击败 90.00% 使用 PHP 的用户

内存消耗 : 21.95 MB, 击败 20.00% 使用 PHP 的用户

Swift

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    func minPathSum(_ grid: [[Int]]) -> Int {
        let m = grid.count
        let n = grid[0].count
        var dp = Array(repeating: Array(repeating: 0, count: n), count: m)
        dp[0][0] = grid[0][0]
        for i in 1..<m {
            dp[i][0] = dp[i-1][0] + grid[i][0]
        }
        for j in 1..<n {
            dp[0][j] = dp[0][j-1] + grid[0][j]
        }
        for i in 1..<m {
            for j in 1..<n {
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
            }
        }
        return dp[m-1][n-1]
    }
}

结果

执行用时 : 21 ms, 击败 85.23% 使用 Swift 的用户

内存消耗 : 15.73 MB, 击败 21.59% 使用 Swift 的用户

Kotlin

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    fun minPathSum(grid: Array<IntArray>): Int {
        val m = grid.size
        val n = grid[0].size
        val dp = Array(m) { IntArray(n) }
        dp[0][0] = grid[0][0]
        for (i in 1 until m) {
            dp[i][0] = dp[i-1][0] + grid[i][0]
        }
        for (j in 1 until n) {
            dp[0][j] = dp[0][j-1] + grid[0][j]
        }
        for (i in 1 until m) {
            for (j in 1 until n) {
                dp[i][j] = minOf(dp[i-1][j], dp[i][j-1]) + grid[i][j]
            }
        }
        return dp[m-1][n-1]
    }
}

结果

执行用时 : 167 ms, 击败 87.04% 使用 Kotlin 的用户

内存消耗 : 36.41 MB, 击败 74.07% 使用 Kotlin 的用户

Dart

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
  int minPathSum(List<List<int>> grid) {
    int m = grid.length;
    int n = grid[0].length;
    List<List<int>> dp = List.generate(m, (i) => List<int>.filled(n, 0));
    dp[0][0] = grid[0][0];
    for (int i = 1; i < m; ++i) {
      dp[i][0] = dp[i - 1][0] + grid[i][0];
    }
    for (int j = 1; j < n; ++j) {
      dp[0][j] = dp[0][j - 1] + grid[0][j];
    }
    for (int i = 1; i < m; ++i) {
      for (int j = 1; j < n; ++j) {
        dp[i][j] = grid[i][j] + (dp[i - 1][j] < dp[i][j - 1] ? dp[i - 1][j] : dp[i][j - 1]);
      }
    }
    return dp[m - 1][n - 1];
  }
}

结果

执行用时 : 294 ms, 击败 100.00% 使用 Dart 的用户

内存消耗 : 148.70 MB, 击败 -% 使用 Dart 的用户

Go

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func minPathSum(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    dp := make([][]int, m)
    for i := range dp {
        dp[i] = make([]int, n)
    }
    dp[0][0] = grid[0][0]
    for i := 1; i < m; i++ {
        dp[i][0] = dp[i-1][0] + grid[i][0]
    }
    for j := 1; j < n; j++ {
        dp[0][j] = dp[0][j-1] + grid[0][j]
    }
    for i := 1; i < m; i++ {
        for j := 1; j < n; j++ {
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
        }
    }
    return dp[m-1][n-1]
}

结果

执行用时 : 5 ms, 击败 43.61% 使用 Go 的用户

内存消耗 : 3.74 MB, 击败 58.48% 使用 Go 的用户

Ruby

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# @param {Integer[][]} grid
# @return {Integer}
def min_path_sum(grid)
  m = grid.length
  n = grid[0].length
  dp = Array.new(m) { Array.new(n, 0) }
  dp[0][0] = grid[0][0]
  (1...m).each { |i| dp[i][0] = dp[i-1][0] + grid[i][0] }
  (1...n).each { |j| dp[0][j] = dp[0][j-1] + grid[0][j] }
  (1...m).each do |i|
    (1...n).each do |j|
      dp[i][j] = [dp[i-1][j], dp[i][j-1]].min + grid[i][j]
    end
  end
  dp[m-1][n-1]
end

结果

执行用时 : 75 ms, 击败 66.67% 使用 Ruby 的用户

内存消耗 : 207.84 MB, 击败 0.00% 使用 Ruby 的用户

Scala

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
object Solution {
  def minPathSum(grid: Array[Array[Int]]): Int = {
    val m = grid.length
    val n = grid(0).length
    val dp = Array.ofDim[Int](m, n)
    dp(0)(0) = grid(0)(0)
    for (i <- 1 until m) {
      dp(i)(0) = dp(i-1)(0) + grid(i)(0)
    }
    for (j <- 1 until n) {
      dp(0)(j) = dp(0)(j-1) + grid(0)(j)
    }
    for (i <- 1 until m) {
      for (j <- 1 until n) {
        dp(i)(j) = math.min(dp(i-1)(j), dp(i)(j-1)) + grid(i)(j)
      }
    }
    dp(m-1)(n-1)
  }
}

结果

执行用时 : 667 ms, 击败 14.29% 使用 Scala 的用户

内存消耗 : 56.80 MB, 击败 100.00% 使用 Scala 的用户

Rust

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
impl Solution {
    pub fn min_path_sum(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut dp = vec![vec![0; n]; m];
        dp[0][0] = grid[0][0];
        for i in 1..m {
            dp[i][0] = dp[i-1][0] + grid[i][0];
        }
        for j in 1..n {
            dp[0][j] = dp[0][j-1] + grid[0][j];
        }
        for i in 1..m {
            for j in 1..n {
                dp[i][j] = dp[i-1][j].min(dp[i][j-1]) + grid[i][j];
            }
        }
        dp[m-1][n-1]
    }
}

结果

执行用时 : 0 ms, 击败 100.00% 使用 Rust 的用户

内存消耗 : 2.40 MB, 击败 65.57% 使用 Rust 的用户

Racket

暂时未解决

1

结果

执行用时 : ms, 击败 % 使用 Racket 的用户

内存消耗 : MB, 击败 % 使用 Racket 的用户

Erlang

暂时未解决

1

结果

执行用时 : ms, 击败 % 使用 Erlang 的用户

内存消耗 : MB, 击败 % 使用 Erlang 的用户

Elixir

暂时未解决

1

结果

执行用时 : ms, 击败 % 使用 Elixir 的用户

内存消耗 : MB, 击败 % 使用 Elixir 的用户